Team_Pigeon The Dropper

Video

Project Summary

Our project attempts to have an agent complete a “Dropper” map, which is a map in which a player attempts to fall safely to the bottom while avoiding obstacles. Our agent will be completing a map in which there is a 5 block wide and 250 block high tunnel made of wool. Inside the tunnel, there are some obsidian obstacles at different locations. At the bottom of the tunnel, there is a pool of water.

The agent will spawn at the top of the tunnel and begin falling from it. The goal of the mission is to let the agent reach the bottom of the tunnel and land in the pool of water safely without taking any damage. In this process, the agent will strafe in the air by moving in different directions to avoid all obsidian obstacles inside the tunnel in order to avoid dying from fall damage and make its way to the bottom.

Approach

Our agent’s actions are currently being rewarded with the following: Reward Function \(R(s)=\left\{ \begin{aligned} 100 &\ (\text{Agent reaches water safely})\\ 1 &\ (\text{+1 For every millisecond the agent is alive})\\ -25 &\ (\text{Hitting an obstacle})\\ \end{aligned} \right.\)

The agent is greatly rewarded with 100 points for completeing the objective and reaching the water safely and is punished for hitting obstacles receiving -25 points. However, we wanted to ensure that the agent wouldn’t spend time randomly moving until it luckily lands in the water or hits an obstacle so we added another reward for staying alive as long as possible in order to encourage the agent to dodge obstacles and get lower in the tunnel. Thus we gave the agent 1 point for every millisecond it remained alive.

To keep simplicity, our agent always faces the north and only takes discrete actions consisting of:

We are primarily using Reinforcement Learning for our approach for the project, using the below DQN algorithm.

\[Q(S_t, A_t)\leftarrow Q(S_t, A_t) + \alpha[R_{t+1} + \gamma\max_a Q(S_{t+1},a)- Q(s_t, A_t)]\]

We used DQN learning to train our agent:

For each episode:
   While the agent hasn't reached the pool of water or dies:
      Choose an action by applying epsilon greedy policy from Q network
      Take the action
      Get the next observation by check the 3*3*10 grid around the agent
      Calculate the reward
      Update Q network

Our agent will take a 10 x 3 x 3 grid of the blocks around it as observation. Since our map is a vertical tunnel and the agent drops from the top of the tunnel, the falling speed of the agent is fast. Therefore, we set the grid so that the agent can ‘see’ 10 levels down in order for it to have enough time to dodge obstacles.

Each episode will see the agent taking the above actions until it reaches a terminal state of either successfully landing in the pool of water or dying from hitting an obstacle. To get the action of each step, we apply the following function from lecture:

\[\pi(a|s)=\left\{ \begin{aligned} \epsilon/m+1- \epsilon \text{ }[\text{ if a*} = argmax_{(a \in A)} Q(s,a)]\\ \epsilon/m \text{ otherwise}\\ \end{aligned} \right.\]

We created an list called action_prob to save the probabilities for each action. Then, we calculate action_prob based on the formula above and randomly choose an action based on the probabilities in action_prob list.

We also experimented another reinforcement learning algorithm called Proximal Policy Optimization (PPO) using the Ray RLlib library. PPO explores by sampling actions according to its latest version of its stochastic policy. This randomness depends on the initial conditions of the environment. The stochastic policy eventually becomes less random and encourages the agent to utilize paths to rewards it has found already.

Currently, we are still working on our approach and are considering changes to other reinforcement learning methods.

Evaluation

Quantitative

We evaluate our agent on its performance with its average score while performing the mission. We expect the agent to receive consistently high scores and to learn how to receive maximum rewards. Over time, we noticed that with our two reinforcement learning algorithms, our agent improves and on average receives a better score.

By using graphs of the return values we can see how effectively our agent is learning with our current reward parameters.

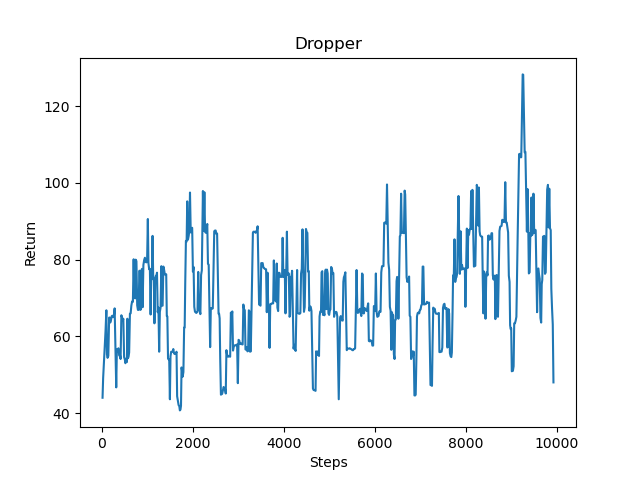
As seen in the graph above, the returns fluctuate quite a bit. This is in part due to the nature of the Dropper. As the agent falls and gets closer to the ground it keeps on gaining points eventually receiving a lot for reaching the water, but should a random action taken due to the e-greedy policy result in its death, the agent loses out on a lot of points and thus has a much lower return value resulting in the many peaks and valleys. Despite this, the graph still shows an overall upward trend, meaning that as time goes on and the number of episodes increases, the agent tends to get farther down and lands in the water much more often.

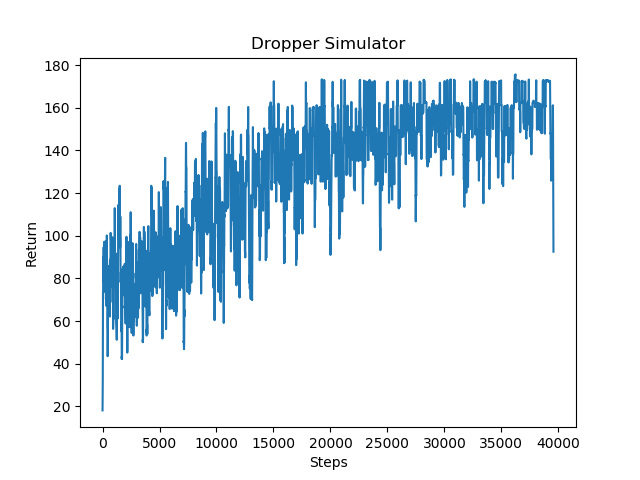
We also recently tried using a different reinforcement learning algorithm called PPO for our agent. Based on the above graph, the results perform somewhat better than the results with the DQN. PPO is said to have a better convergence and performance rate than a simple DQN model, and it is can be seen that over time the agent performs a bit better. However, it is important to note that the PPO algorithm was run much longer than the DQN algorithm, so while it may yield better results it is much slower.

Qualitative

It can be seen that the agent begins taking random moves with a high probability of failing the mission. Over time, gradually the agent learns to dodge the obstacles and succesfully finish the mission.

Remaining Goals and Challenges

Resources Used

CS175 Assignment 2’s DQN algorithm

https://github.com/microsoft/malmo

http://microsoft.github.io/malmo/0.30.0/Documentation/

https://docs.ray.io/en/latest/rllib-algorithms.html#ppo

PyTorch library